Temporal Difference Control in Reinforcement Learning

Temporal Difference learning is one of the most important idea in Reinforcement Learning. We should go over the control aspect of TD to find an optimal policy. We should apply the Generalized Policy Iteration (GPI) framework with two types of control:

• Sarsa: On-policy TD Control
• Q-learning: Off-policy TD Control
• Expected Sarsa: Off-policy TD Control with expected return over any policy

Sarsa: On-policy TD Control

Sarsa stands for “State, action, reward, state, action” because we are trying to estimate the state-action function Q(s, a) over state-action pair.

• This is very similar to the state-value function update during the TD prediction.
• Note that a policy pi is implicit here although it’s not labeled in the update formula.
• Update is done every transition from a nonterminal state s.
• To apply GPI, we use epsilon-greedy or epsilon-soft policy to optimize the policy, while improving the estimate of Q(s, a) simultaneously

Example: Windy Gridworld

Applying Sarsa to solve this problem of getting from S to G in the grid with upward windy.

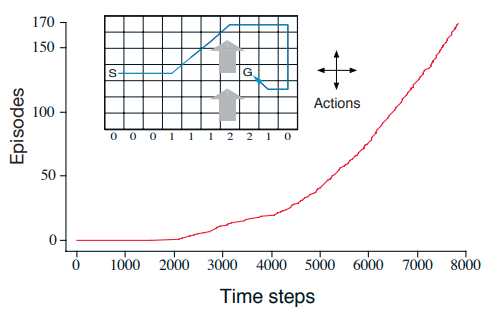
• The plot show the total number of time steps vs total number of episodes
• Note that the slope of the curve is very flat. It means it takes a long time to complete an episode initially
• Toward the end, the curve should converge to a straightly in where each episode runs for 15 steps as the optimal solution.
• Monte Carlo method is not a good fit for this problem because many policies will not find the solution and thus an episode will run forever. It won’t learning anything until an episode is finished.

Q-learning: Off-policy TD Control

The Q-learning algorithm is a online learning algorithm.

This is very similar to Sarsa except Q-learning uses a max instead of the next state-action pair. It’s analogous to the bellman equation for DP.

Comparison with Sarsa

• Sarsa is sample based algorithm to solve the standard Bellman equation for state-action function.
  • It also depends on a policy which guides to generate the trajectories
• Q-learning is a sample based algorithm that solves the Bellman optimality equation to learn Q(s, a)
  • No need switch between evaluation and policy improvement
  • Directly learn Q*

Why is Q-learning off-policy?

• Q-learning bootstrap off the largest action value in its next sate. This is like sampling an action under an estimate of the optimal policy rather than the behavior policy.
  • Q-learning’s target policy is always greedy with respect to its current values
  • Its behavior policy can be anything such as epsilon-greedy.
• Q-learning does not need to use importance sampling.
  • Because Q-learning learns the optimal action-value function directly.
  • Since the target policy is greedy, the expected return from the state is equal to a maximal action value from that state (all other probability is zero).
• Subtleties of directly learning of Q()
  • Although the optimal policy is learned. The exploratory nature of the epsilon-greedy behavior policy still causes agent to take suboptimal move, causing the estimate of the return to be lower.
  • So Sarsa have better performance online because it accounts for its own exploration (learn safer path, although not the optimal path)

Expected Sarsa

Explicitly computes the expectation over the next actions under the policy’s probability.

• The expected value update is much more stable than Sarsa (lower variance)
• More computation cost with more actions

Expected Sarsa can be generalized to off-policy learning

• The policy used can be a different target policy policy (this target policy can be any policy).
• If it’s a greedy target policy, then it’s the same as Q-learning. So Q-learning is a special case of Expected Sarsa.

Expected Sarsa is insensitive to the step size unlike the Sarsa.

Reference: most of the material of this post comes from the book Reinforcement Learning