Knowledge Distillation (introduction)

Problem

Large ML model might be difficult to be deployed because of deployment constraint (edge/mobile devices). Training a small model on raw data might not achieve as high accuracy as training a large model.

• Large models tend to be complex
• We don’t want complex model, but we want sophisticated model (know the relevant details to make prediction)
• How do we just capture the minimal relevant information for inference more efficiently?
• Is it possible to distill/condense this knowledge into a small model?

Solution

Knowledge distillation might be something that you can try.

• Also known as teach and student networks
• Another complexity reduction technique like network pruning
• Steps
  • Train a large complex model to achieve best accuracy
  • Use the large model as the teacher to generate labels to train a smaller model(s) as the student model
  • Deploy student in production for inference
• Student model is a form of knowledge transfer
• Soft target – p-distribution generated by teacher
  • Note that we don’t use the hard label from the teach model (ie 100% on the highest probability class)
  • Student model tries to learn the soft distribution coming from the final softmax layer of the teacher model
  • Student model has different object function
• Softmax temperature (T)
  • Improve the softness of the teacher’s output distribution
  • Often the teach model’s softmax layer is already quite confident with one class close to 100% and all other classes close to 0%. This does not provide much difference from directly using the ground truth label
  • 
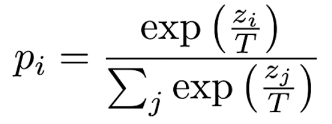
  • When T=1, p is the standard softmax. As T increases, the probability to more evenly distributed to all classes.
  • This is referred as the “Dark Knowledge”, which is what we want the student model to learn
• Keras API
  • student_loss_fn – against the hard label
  • distillation_loss_fn – against the soft teach distribution
    • Use KL divergence to compare student and teach output distribution
      • Loss = (1-alpha)*Loss_hard_label(student_loss) + alpha*Loss_KL(distillation_loss)
      • alpha = how much to match to the teacher’s distribution as opposed to the ground truth
  • temperature – softening teach softmax distribution
• Result
  • In Distilling the Knowledge in a Neural Network, the distilled model achieves higher performance by learning from an 10xEnsemble model compared to a baseline model that is directly trained on the data
  • 
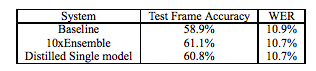
• Not necessarily single teach, can be multiple
  • Model Compression with Two-stage Multi-teacher Knowledge Distillation for Web Question Answering System
  • Combine ensembling and knowledge distillation
    • Pretrain student model with distillation
    • Finetune student model with teacher distillation
• Not necessarily smaller student model than teacher
  • In a case study, a larger student noisy model can use distillation to achieve robustness from a smaller teacher model