Dimensionality Reduction in Machine Learning

Problems of high dimension

• Many ML algorithm relies on distances to compute similarity between samples
• Curse of dimensionality – as number of dimension increases, distances between any two sample from the dataset tends to be more alike (more concentrated) in a way that makes it hard to differentiate them. Every point is point is roughly in similar distance to each other, which results in more difficulty in grouping/cluster the samples
• Risk of overfitting – the model might try to fit to the irrelevant features (noise) just because of some noise in the training set but such relationship is not present in the validation/test data set
  • Can even add more noise during prediction phase for testing
• Resource waste – more features means more columns of data to store/process/maintain
• Performance – the extra features can cause more time to process for an online system
• Redundant features can cost problem of collinearity
  • which is harmful to some model like linear regression
    • it’s hard for the model to be confident in the coefficients of two high correlated features, which results in high p-value of both coefficients
• Features space grows exponentially for each feature added, which requires a lot data to train
  • Feature space become sparse
  • 
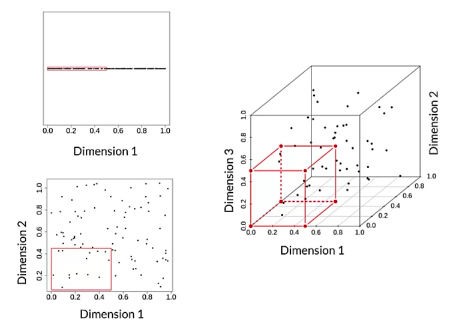
• The Hughes effect – as number of dimension increases, it’s harder to find correct hypothesis (because the hypothesis space is larger) and it needs more examples to generalize

Algorithms

• Latent Semantic Indexing/Analysis (LSI/LSA)
  • Unsupervised
  • Single Value Decomposition (SVD)
    • For decomposing non-square matrix A = S*V*D
    • Reconstruct original matrix with few dimensions
• Principle Component Analysis (PCA)
  • Only for square matrices
    • Eigen value decomposition
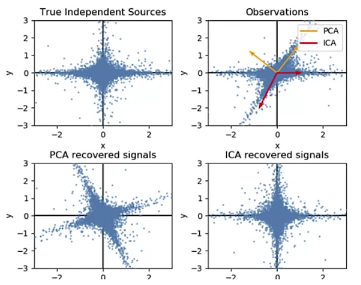
• Independent Component Analysis (ICA – paper)
  • Separates multivariate signal into addictive components that are maximally independent
  • Used for separating super-imposed signals
  • Difference with PCA
    • PCA – looks for uncorrelated factors
    • ICA – looks for independent factors (a factor is uncorrelated to any other factors)
    • Not result in orthogonal components like PCA
  • Removes high order dependence
    • 
• Non-negative Matrix Factorization (NMF)
  • Sample features need to be non-negative
• Latent Dirichlet Allocation (LDA)

Other dimension reduction technique

• Quantization
  • This is a technique rather than a specific algorithm
  • Benefit
    • Lower cpu/gpu/memory/power consumption
    • Faster inference performance/latency
    • Made possible to run on mobile/embedded devices
  • Disadvantage
    • Might lose precision
    • Values might be saturated/clipped if the quantization range is not set up correctly
  • Quantize the input
    • Ex: reduce a color image to a gray scale or even black and white image.
  • Quantize model weight
    • Use lower precision model weight and operations (float -> 8 bit)
    • Input support is more available in embedded devices
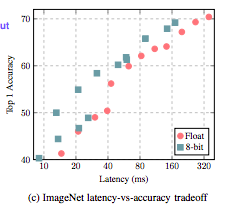    • from: Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
    • Type of model quantization
      • Quantize model post training (support in Tensorflow Lite)
        • Very simple to apply
      • Quantization aware training (in Tensorflow)
        • Need to add fake quantization nodes during training (see two “quant” nodes below)
        • 
• Pruning
  • 
  • Cutting out nodes/edges in a neural network.
  • Reduces number of parameters (small model to store)
  • Reduces number of edges/connections (fewer operation to process)
  • Act as a form of regularization
  • Weight pruning based on magnitude during training
    • Slow ramp up pruning using a schedule until desired sparsity is reached
  • Lottery ticket hypothesis
    • An over-parameterized network contains a subnetwork that perform as well as the entire network
    • Observation: Post pruning + fine tuning might worse than just using original weights
    • There is a subnetwork that “won the lottery”
  • Sparse tensor in tensorflow

The unavoidable

Sometimes you just have to use a large model to squeeze every bit of performance. You might need to use distributed training when the model is too large to fit in a machine (Training large models – distributed training)