KL Divergence vs Cross Entropy in Machine Learning

The KL (Kullback–Leibler) Divergence is frequently mentioned in the field of machine learning. It measures the similarity of the two distributions P and Q.

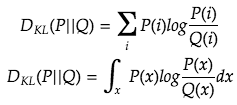
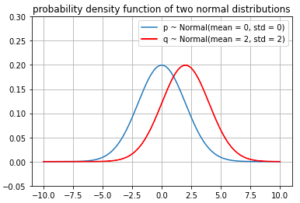
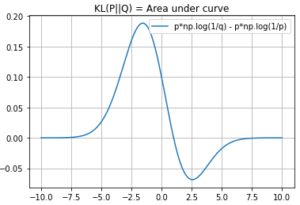
But we rarely see the KL divergence used as an optimization objective, but rather we see cross entropy used often. We will give an intro to KL divergence and see why the KL divergence is relevant in ML?

What is KL Divergence really?

See an illustration to get some intuition about KL Divergence (skip this part if you only care about its relationship with Cross Entropy)

What is P and Q notation?

• P is the actual distribution.
• Q is the predicted distribution

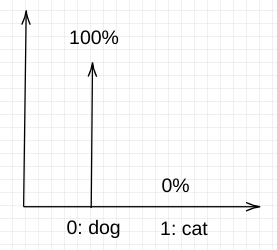
Example: in an image classification problem of dog-vs-cat, you can think of the distribution over two classes (dog and cat). For a given set of features (ie for a given image), you would assign 100% to the label of the image and 0% to the other classes.

Example

We assign class 0 to dog and class 1 to cat.

Ground truth labels are usually set up as below for the classification problem (1 from many)

• A dog labeled image will have a distribution P = [100%, 0%]
• A cat labeled image will have a distribution P = [0%, 100%]

Distribution P:

Prediction (predicted label by model):

During prediction, the model might predict a distribution Q = [90% 10%] which means it’s 90% confident the image is a dog and 10% to be cat.

Distribution Q:

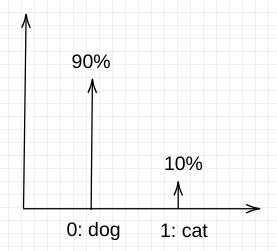
Given the distributions P and Q above, KL divergence can be calculated on all possible images (features) and averaging over all the individual KL divergence.

Observation: want to have P = Q as much as possible

When the distribution P is the same as Q, the KL divergence equals to 0 because log(1) = 0.

In the same dog-vs-cat example, when P = [100% 0%], Q = [100% 0%] for an image, then the KL divergence is 0. When there is a large number of images, this might be not be possible in practice, but it means the closer that Q is similar to P, the lower the KL divergence would be. In this sense, KL divergence is a metric that we can optimize for.

How is Q related to a ML model?

Q is the distribution of the classes. However, Q is not a fixed distribution. When you consider Q(features) as a function of the feature of one image, Q is the ML model that you are training. Think about the softmax output of your neural network or logistic regression. Q(features) output the distribution which is the prediction. The model training process is to optimize Q via changing the model parameter to be close to P over the available data. This is achieve by minimizing the KL divergence.

Why do we minimize the cross entropy instead of the KL divergence in ML?

The cross entropy is often called the negative log likelihood. It’s the most widely use optimization object for classification problem while we want to predict the most likely class given a sample of features. Why do people use cross entropy instead of KL divergence? It turns out they are optimizing the same thing.

We can rewrite the KL divergence as followed in the discrete case:

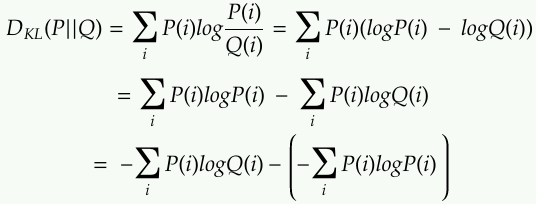
You can recognize the tems as the entropy and cross entropy.

• log of a probability (<=1) is always negative
• the negative side ensure the entropy and cross entropy are >=9

Given a ML problem, the actual distribution P of the underlying data does not change, so we can treat Entropy(P) as a constant. What we have control over is the function Q which changes when update the model parameters. In other words, minimizing the KL divergence by updating Q is the same as minimizing the Cross Entropy by updating Q.

Side note: In this problem setting of MLE (maximum likelihood estimation), there is really no difference between minimizing KL divergence or the Cross Entropy. However in Bayesian Inference (Variational Inference), we cannot just minimize the Cross Entropy but the ELBO (evidence lower bound) instead (link).

Can KL divergence be negative?

No because the cross entropy H(P,Q) is always greater than or equal to the entropy H(P)

• KL divergence is minimized when P=Q, which is when cross entropy (P||Q) is minimized to be the same as the pure entropy of P
• In other words, even if all the prediction uncertainty (AKA. reducible/systemic/epistemic/ignorance of agent/lack of data) is removed, in which we have obtained the best possible model, but we are left with the unreducible uncertainty (AKA. aleatoric/statistical/stochastic/inherent/by-chance).