Tutorial: Cross Entropy and Negative Log Likelihood

Cross Entropy and Negative Log Likelihood are the same thing, but I would like to explain why they are called that way to make them easier to understand.

Cross Entropy

It is defined on between two probability distribution p and q where p is the true distribution and q is the estimated distribution.

Let’s break it down word by word.

Entropy measures the degree of randomness, and it’s denoted by the formula below:

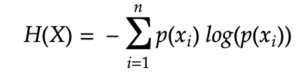
For example, consider the roll of a six sided dice.

Case 1: For a fair dice, the is distribution can be represented as

[1/6, 1/6, 1/6, 1/6, 1/6, 1/6] over the possible outcome of [1, 2, 3, 4, 5, 6]

H(X) = -1/6*log(1/6) - 1/6*log(1/6) - 1/6*log(1/6)  
       -1/6*log(1/6) - 1/6*log(1/6) - 1/6*log(1/6) = 1.791

Case 2: consider the roll of a unfair dice that is more biased to rolling a 6, with distribution

[0.1, 0.1, 0.1, 0.1, 0.1, 0.5] over the possible outcome of [1, 2, 3, 4, 5, 6]

H(X) = -0.1*log(0.1) - 0.1*log(0.1) - 0.1*log(0.1) 
       -0.1*log(0.1) - 0.1*log(0.1) - 0.5*log(0.5) = 1.289

Case 3, consider an extremely unfair dice that is very heavily biased to rolling a 6, with distribution

[0.01, 0.01, 0.01, 0.01, 0.01, 0.95] over the possible outcome of [1, 2, 3, 4, 5, 6]

H(X) = -0.01*log(0.01) - 0.01*log(0.01) - 0.01*log(0.01) 
       -0.01*log(0.01) - 0.01*log(0.01) - 0.95*log(0.95) = 0.279

As you can see, Case 1 with the most “randomness” has the highest entropy while Case 3 with least “randomness” has the lowest entropy. Hopefully you are convinced that the formula for Entropy H(X) measures the randomness.

Cross refers to the fact that it needs to relate two distributions. It’s called the cross entropy of distribution q relative to a distribution p.

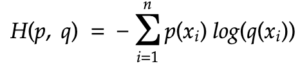
What is changed from the formula for entropy H(X) is that now the argument of the random variable X is replaced by p and q. It might be confusing at first, but the reason we cannot use X in this case is that both p and q are distribution of X.

• p is the true distribution of X (this is the label of the y value in a ML problem)
• q is the estimated (observed) distribution of X (this is the predicted value of y-hat value in a ML problem)

For example, consider another dice example. It’s observed in the data set that the outcome is distribution is

[0.18, 0.18, 0.15, 0.17, 0.17, 0.15] over the possible outcome of [1, 2, 3, 4, 5, 6]

Case 1: Let’s say we have a belief that the dice is fair so that its true distribution should be

[1/6, 1/6, 1/6, 1/6, 1/6, 1/6] over the possible outcome of [1, 2, 3, 4, 5, 6]

We can calculate the cross entropy as

H(p, q) = -1/6*log(0.18) - 1/6*log(0.18) - 1/6*log(0.15) 
          -1/6*log(0.17) - 1/6*log(0.17) - 1/6*log(0.15) = 1.7946

Case 2: If the dice is believed to be biased so that its true distribution is

[1/10, 1/10, 1/10, 1/10, 1/10, 5/10] over the possible outcome of [1, 2, 3, 4, 5, 6]

We can again calculate the cross entropy as

H(p, q) = -1/10*log(0.18) - 1/10*log(0.18) - 1/10*log(0.15) 
          -1/10*log(0.17) - 1/10*log(0.17) - 5/10*log(0.15) = 1.8356

Since Case 1 has a lower cross entropy than Case 2, we say that the the true probability in Case 1 is more similar to the observed distribution than Case 2.

Negative Log Likelihood (NLL)

It’s a different name for cross entropy, but let’s break down each word again.

Negative refers to the negative sign in the formula. It seems a bit awkward to carry the negative sign in a formula, but there are a couple reasons

• The log of a probability (value < 1) is negative, the negative sign negates it
• Most optimizer software packages minimize a cost function, so minimizing the negative log likelihood is the same as maximizing the log likelihood.

Log refers to logarithmic operation on the probability value. Why do we need to use log function? The reason is a bit beyond the scope of this post, but it’s related to the concept in information theory where you need to use log(x) bits to capture x amount of information.

This blog says the reason is for numerical stability on computer.

Why we want to wrap everything with a logarithm? Computers are capable of almost anything, except exact numeric representation.

I disagree because the numerical stability is a result/byproduct rather than the reason to use log in negative log likelihood.

Likelihood is meant to be distinguished from probability.

• Probability is the chances that some data is observed with some value given some underlying model (parameters of the distribution).
• Likelihood is the chances that the parameters of the model taken on certain some value given the observed data.

In terms of the formula, it looks just like a probability but the interpretation and usage is different.

So the NNL is defined as below

Next we can apply the independence of each sample to turn it into log of a product, and then apply log(a*b) = log(a) + log (b)

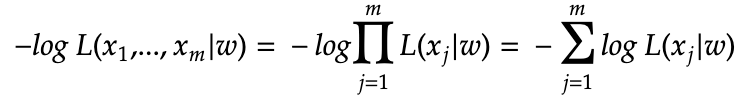
The NLL presented so far does not really look like the cross entropy formula, the main reason is that the above summation is based index j which is the sample index, while the early cross entropy formula’s summation has an index_i which is based on the each possible values in the discrete sample space.

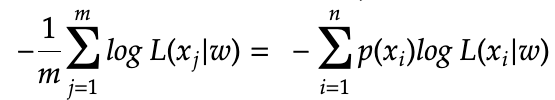
In the above equation, we first added a normalization factor 1/m in front, then we switch the summation from being “over the individual sample” to “over each distinct values of the sample space”. In the dice roll example, m is averaging over the number of times we roll the dice in the experiment and n=6 for the 6 possible outcomes.

Next we should see the likelihood function as a probability function because w depends on the model chosen and the observed samples that fit the model parameters

So all the details of w (the model and the parameters) is embedded into the form that q(x) takes because q(x) is really a short hand for q(x|w). In our example of dice roll, the discrete probability distribution observed has some weights over the possible outcome of [1,2,3,4,5,6], and these weights can be considered as w of the model.

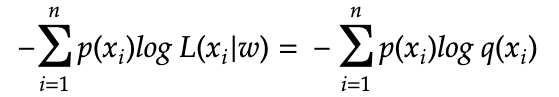
In this sense, we have gone back from likelihood to probability. And we see that NNL is the same as cross entropy.