How public key encryption works at the high level:

• User A tries to send a message (ex: “My favorite food is banana”) to user B over the internet.
• User A does not want anyone else to be able to read the message other than user B.
• User A first asks user B for B’s public key (a large number).
• User A uses this public key to encrypt the message, which turn into an encrypted message (ex: “aoipsdfa;skldj%13asidof&%”), and then send the encrypted message to user B.
• While the message is being sent over the internet, hackers would be able to read the encrypted message but is not able to understand because he cannot decrypt it.
• On the other hand, user B receives the message and is able to decrypt it using B’s private key for decryption, recovering the original message.

Encryption and decryption in action

How does the encryption and decryption work algorithmically?

One commonly used technique is the RSA (https://en.wikipedia.org/wiki/RSA_(cryptosystem)).

Below is a demo of a toy example of apply RSA.

Step 1) User B generates Public Key and Private Key

User B first generates a pair of keys: public key and private key.

• Public key is published by user B and is viewable by everyone on the internet.
  • Let’s denote this public key with the letter “e” because it stands for encryption key, as it’s used by other user A (or other users) to send encrypted message to user B.
  • User B also publish a number n.
• Private key is generated by user B but is not shared with anyone else.
  • Let’s denote this private key with the letter “d” because it stands for decryption key, as it’s used by user B to decrypt the encrypted message from user A.

In this above example, let’s assume the following

• e = 17
• d = 413
• n = 3233

We will explain how e, d, and n are chosen later

Step 2) User A encrypts the message

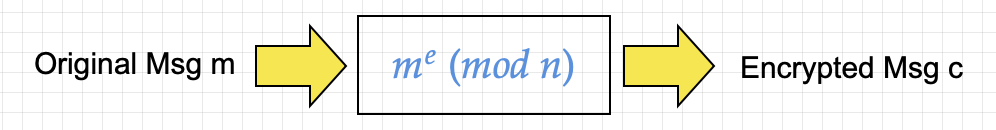
• The text “My favorite food is banana” needs to be converted to an integer first.
• Normally this text can be quite long and we will need to chuck the text into smaller piece to work with.
• Let’s restrict to the first letter “M” in our toy example and “M” maps to 13 because it’s the 13th alphabet.
• Next we apply the formula m^e (mod n) = 13¹⁷ (mod 3233) = 47
• So the encrypted message 47 is sent to user B

Step 3) User B decrypts the message

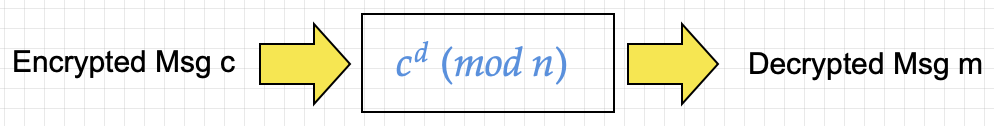
• User B applies the decryption formula c^d (mod n) = 47⁴¹³ (mod 3233) = 13
• The integer 13 maps back to the letter “M”. (Wow how did that work? What is the magic in the modulus formula and the parameters e, d, and n? Please keep reading :P)

The process of Step 2 and 3 can carry on for each block of text (in this toy example, each block is just 1 character).

About text length.

In practice, RSA can handle long strings (ie 1024 or 2048-bit) so we can encrypt a short message like a password without problem. If the text is indeed much long, we don’t directly use RSA but a hybrid approach (https://en.wikipedia.org/wiki/Hybrid_cryptosystem)

How are public key and private key chosen?

We first start with two distinct prime number p and q (these 2 numbers are also secret to user B)

• p = 61
• q = 53

Then we compute n = p * q = 61 * 53 = 3233

Calculate LCM (least common multiple) of p-1 and q-1

• lcm(p – 1, q – 1) = lcm (60, 52) = 780

Choose any number 1 < e < 780 that is coprime to 780. (coprime means “not sharing any common factor”)

• Let e = 17

Calculate d as the modular multiplicative inverse of e (mod lcm).

• Modular multiplicative inverse: a and b are modular multiplicative inverse if (a*b) (mod n) = 1d
• Want (d * e) (mod 780) = 1
• so (17 * d) (mod 780) = 1
• Since (17 * 413) (mod 780) = 1, so d = 413
• How to solve for d = 413?
  • d = e^{lcm – 1} (mod lcm) = 17^780-1 (mod 780) = 413
  • This above method is an application of Euler’s theorem:
    • Given e=17 is coprime to 780, that is gcd(17, 780) = 1, then
    • 17⁷⁸⁰ = 1 (mod 780)
  • Next we just play round this equations to get the inverse (non-vigorously):
    • Next we just factor out 17 on both side
    • 17⁷⁷⁹ * 17 = d*17 (mod 780) where we replace the right side of the equality with d*17 which is 1 (mod 780)
    • So by d = 17⁷⁷⁹ (mod 780)
  • Note that the modular multiplicative inverse is not guaranteed to exist but in our case here it’s guaranteed because we have e (17) being coprime to n (780)

The public key is (n=3233, e=17), and user A can encrypt the message with n and e.

The private key is (n=3233, d=413), and user B can decrypt the message with n and d.

Applying the public and private keys again

It works because of the modulus operations

• Let original message be m
• User A generates encrypted message c = m^e (mod n)
• User B decrypts the encrypted message by raising to power d and modulus n:
  • c^d (mod n) = (m^e)^d = m (mod n) because e and d are modular multiplicative inverse.