I would like to show you all the properties, formula, and neat formulas about the Gaussian distribution that I have encountered in machine learning.

Probability density function (PDF) of 1-dimensional Gaussian:

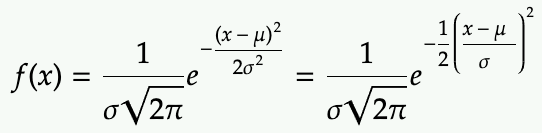
where sigma is the standard deviation and mu is the variance.

Property: the pdf integrate to 1.

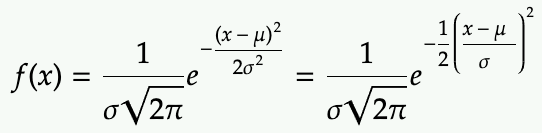
This might be obvious but sometimes you need to be able to recognize this when it’s presented in an modified form. For example,

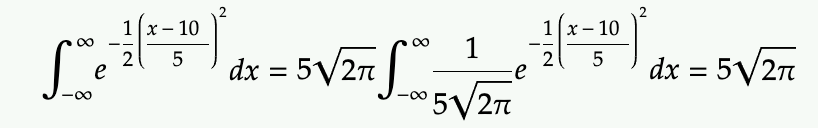
This integral takes some work to figure out, but if you recognize the Gaussian pdf form where sigma=5 and mu=10, you can factor out the normalization factor for the PDF to integrate to 1.

Property: sum of Gaussians is Gaussian

More precisely, if we have two independent random variables X and Y each following Gaussian distributions

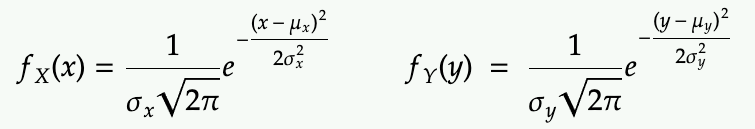
We define Z = X + Y, and we use the properties

• mean of Z is the sum of the means of X and Y (regardless of X and Y are independent or not)
• variance of Z is the sum of the variances of X and Y (only when X and Y are independent)

then Z is distributed as the following

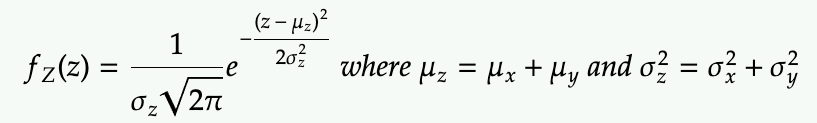
Note that the above can be applied to difference as the subtraction is the same as adding the negative.

If Z = X – Y, then the only difference is that mean of Z:

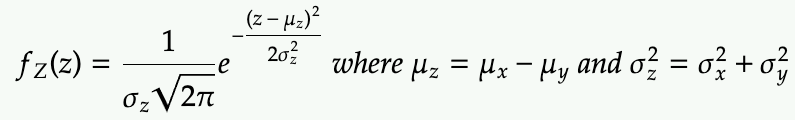
Property: Gaussian is maximum entropy of all distribution with fixed mean and variance

PDF of multi-dimensional Gaussian (multivariate normal distribution)

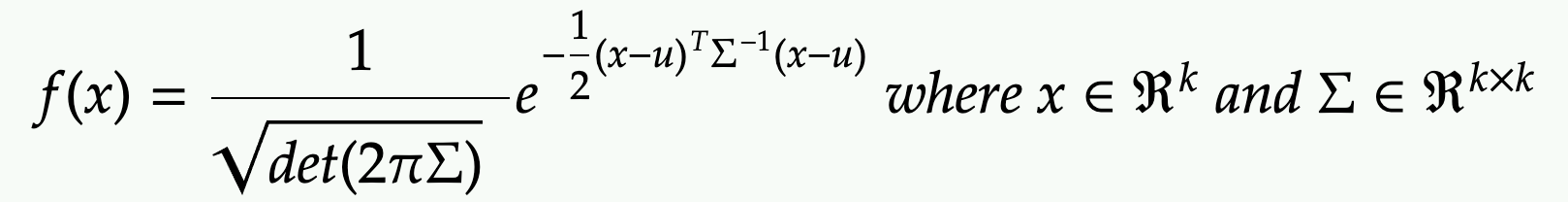
where x and mu are k-dimensional vector and Sigma is k-by-k covariance matrix.

Sometime it’s writer in slightly different notation

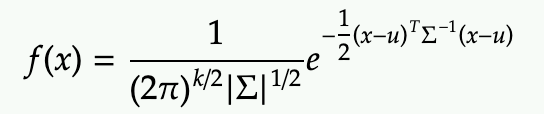
When k=2, it’s also written without the matrix notation as:

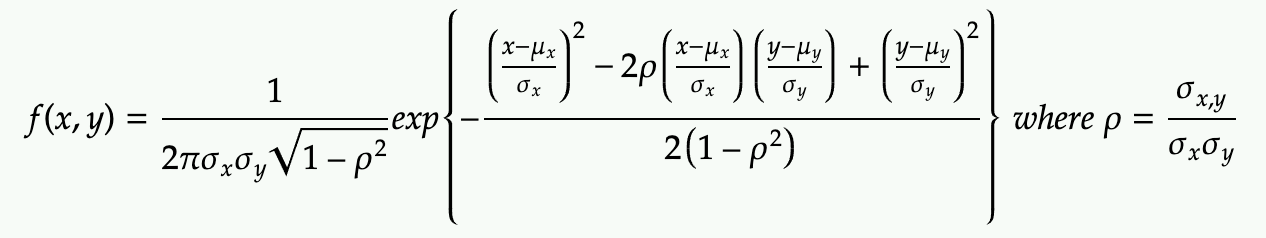
How is this form related to the matrix form above? Hints are below but we will skip all the algebra here:

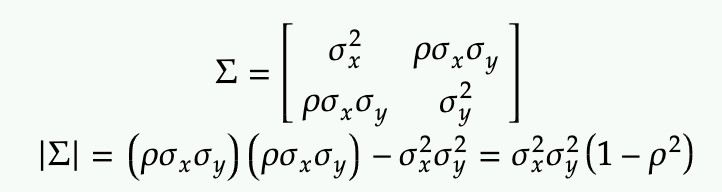
Property: Marginalizing 2-Dimensional Gaussian results in 1-Dimensional Gaussian

Ex: we try to marginalize the x dimension by integrating over it so that the resulting Gaussian is only a function of y

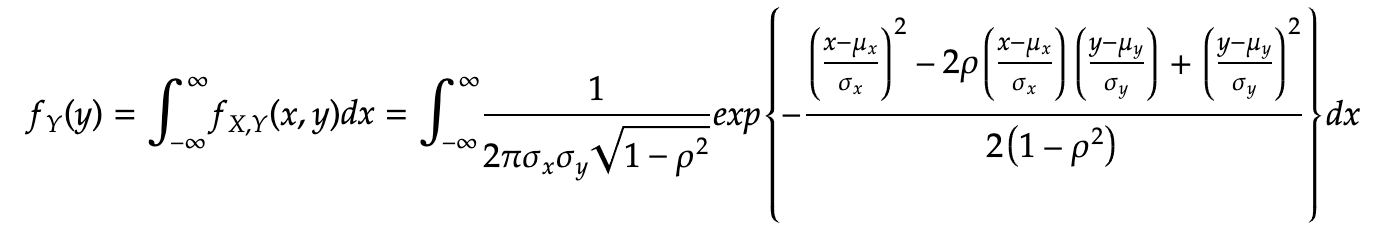
then you need to some tedious algebra with (completing the square and expression rho with the sigmas, see link)

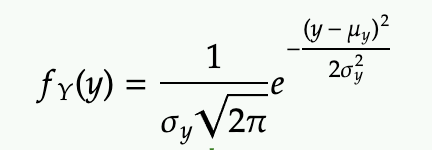
which is simply a 1-D gaussian of y. Note the correlation coefficient (rho) absorbs all the mess and everything comes out cleanly (how nice!).

Property: Marginalizing k-Dimensional Gaussian results in (k-1)-Dimensional Gaussian

This is really just an extension of the 2-D case into k-D with matrix notation. We start again with this standard definition

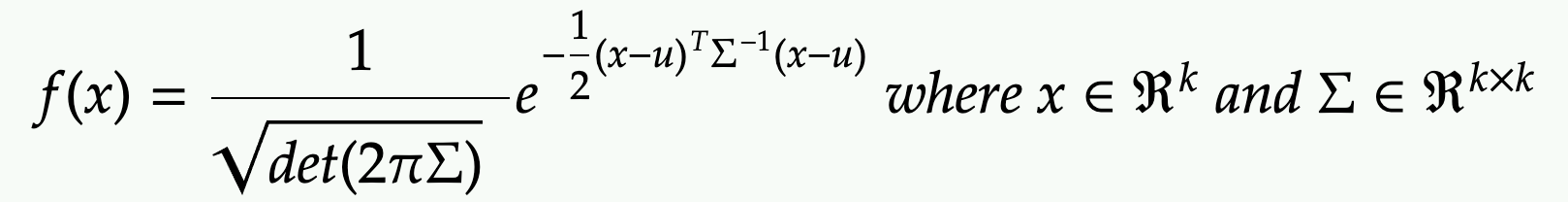
To marginalize the i-th dimension, we are basically chopping of this dimension in the the mean

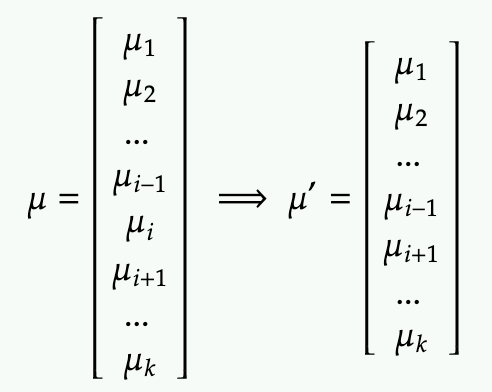
We also need to chop off the i-th column and i-th row from the covariance matrix

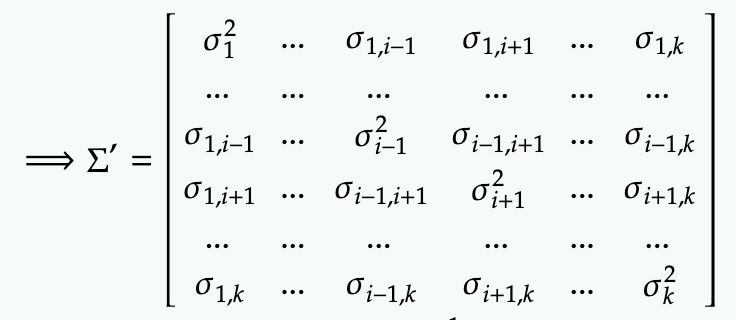
The resulting is distribution is a Gaussian of (k-1) dimension

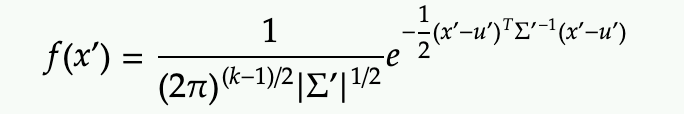
Conditional PDF

Property: Conditioning 2-Dimensional Gaussian results in 1-Dimensional Gaussian

To get the PDF of X by conditioning Y=y₀, we simply substitute it

Next trick is only focus on the exponential term and refactor the x terms and try to complete the square for x (with some messy algebra).

• substitute the rho back with the covariance
• multiply by the variances of x in both the numerator and denominator

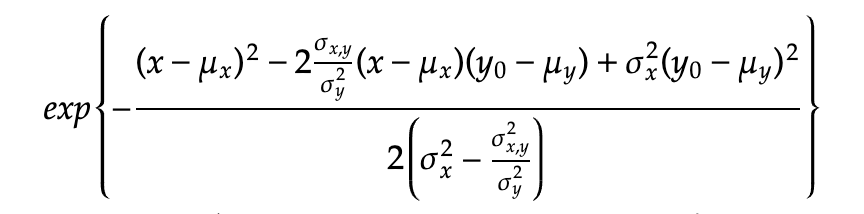
Then try to set up the x terms to complete the square in term of x

Rewrite with by actually completing the square

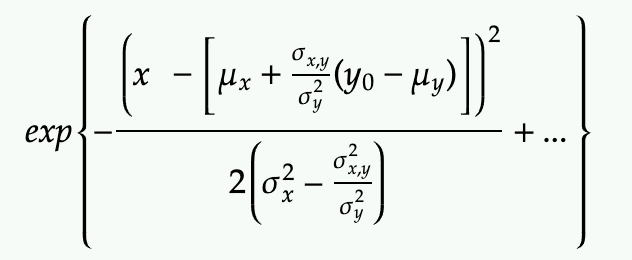
We can directly derive the mean and variance of the resulting Gaussian PDF of x conditional on y

Property: Conditioning n-Dimensional Gaussian on (n-k)-Dimension result in k-Dimensional Gaussian

This is a generalization of the 2-D case, so we would use matrix notation.

First we define a n-Dimensional Gaussian where we denote the first (n-k) dimensions as x and the last k dimensions as y

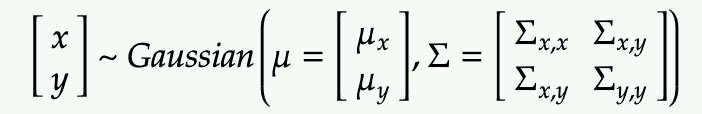
First, we can write out the exponential term in the join Gaussian

Note that the covariance matrix can be rewritten in block inverse form with the Schur Complement:

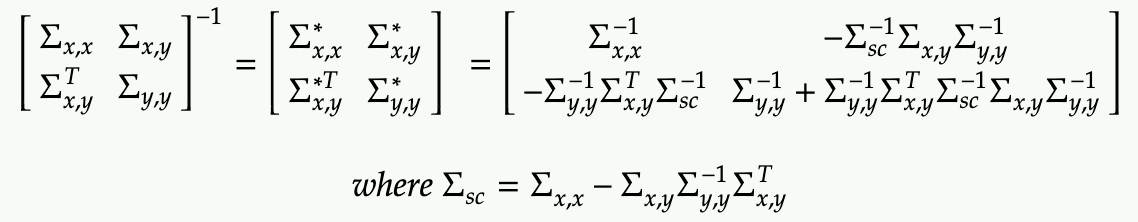
Next, multiply out the terms inside the exponential fully and complete the square for x (in matrix term).

From the form above, we can recognize the mean vector and covariance matrix in terms of x in the first term before the addition:

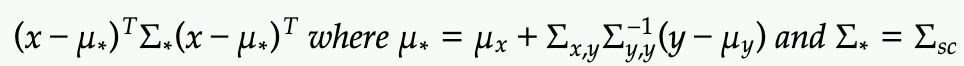
Alternatively, we can apply f(x|y)=f(x,y)/f(y). In this form, the exponent can show derived similarly by subtracting off the exponential term of the marginal PDF of f(y)

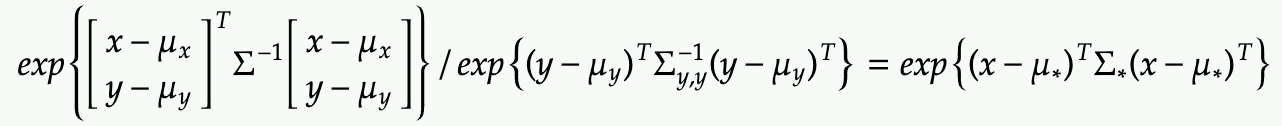
Either way, x given y is distributed according the mu* and sigma* above.

I have skipped a lot of details and I encourage you to check out the derivation here