Tabular vs Function Methods
In reinforcement learning, there are a few methods that are called tabular methods because they track a table of the (input, output) of the value functions
- Dynamic Programming
- Policy Iteration
- Value iteration
- Generalized policy iteration (GPI)
- Monte Carlo Method
- Temporal Difference
- Q-learning (Off-policy TD)
- Sarsa (On-policy TD)
However when the state space is enormous that it cannot be tracked in a table. We can use parameterized functions to approximate these value functions.
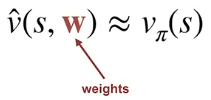
- Weight representation is more compact than enumerating all values
- Note that when a weight changes, it can affect multiple outputs (this is similar to supervised-learning)
Linear value function approximation

- The value is approximated using a linear combination of the features
- There are some limitation of expressiveness of linear functions but we can be more creative in making new features
- Tabular value functions are a special case of linear functions
- Use one weight for each state
Non-linear value function approximation
- Neural network is an example
Generalization and Discrimination
- Generalization: update to value of one state affect value of other states
- Able to recognize some states are similar to treat them similarly (update both)
- Extreme generalization: aggregate all state and predict the average
- Discrimination: ability to make value of two states different
- Tabular methods have high discrimination since it treat each state independently
- Need to find a way to balance the two and make trade-off
Estimate Value Functions as Supervised Learning
- Can we estimate the value functions as a supervised learning problem?
- Supervised-learning
- Target is fixed. RL has non-stationary target:
- The environment/policy is not stationary
- In GPI, we lean the policy and value-function. The target values are nonstationary because of bootstrap.
- Training examples are batched (not online, temporally correlated)
- Target is fixed. RL has non-stationary target:
- Monte-Carlo method can be framed like supervised learning
- One (state S, return G) mapping for each episode
- Learn a value function of a given policy
- Why MC is not supervised learning?
- Because MC is temporally correlated
- TD can be framed like supervised learning but additional completely than MC
- Also have (state S, return G) mapping
- But return G depends on w (target is not fixed)
Value Error Objective

- We want to measure the error between value function approximation and the true value function
- It needs to be weighted different across the state-space using mu(s)
- mu(s) is often the time spent in state s, known as on-policy distribution
- stationary in continuing tasks
- in episodic tasks, mu(s) can depend on the initial state
- mu(s) can be defined as the time spent in each state following the policy pi
- We would like to minimize this value error function by adjusting the weights w
- Can use gradient descent
- The gradient descent step is followed with Ut replacing v_pi(s) because we are using Ut as an estimate of v_pi because we don’t have true v_pi
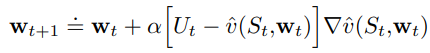
- If Ut is unbiased, then expected of Ut is v_pi, then we are guaranteed to converge.
- For linear value function approximation, the gradient is just the feature (each weight corresponds to a feature)
- Even the function that minimizes the error does not mean it’s the true value function
- Reason is that the function might not correspond to the true value function (limited by the choice of function parameterization and choice of objective/features/functional form)
Gradient Monte for Policy Evaluation
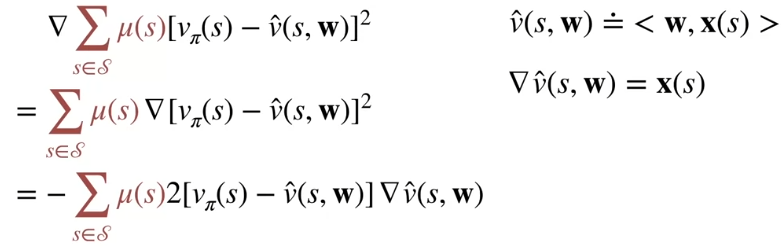
- Gradient is quite easy to calculate when the approximation function is linear
- Summing over all states is usually not possible, also hard to know the distribution mu(s)
- We can make small update each time over the sequence of (state, value) following a policy pi
- Each step is an update (a form of stochastic gradient descent)
- Since we don’t have v_pi(s), we can use the sampled return G given state s (G is unbiased estimate of v_pi(s))

- State Aggregation
- when we update the state-value for one state, the state-value for all the states in the same group is updated
- it’s a form of linear approximation (the group one-hot variable is the feature)
- Example of a random that takes 100 steps to the left or right of [0, 1000] range. The states are aggregated into 10 states from 1000 states.

Semi-gradient TD(0) – biased target

- Replace the return estimate with a biased estimate that depends on w (bootstrapping estimate of vi_pi(s))
- It’s not guaranteed to converge because the bootstrapping estimate produces part of a gradient (but something extra depending on w). It’s called semi-gradient methods.
- However,
- it usually converge quicker because variance is lower
- it also enables continual and online learning
In the same 1000-state random walk example,
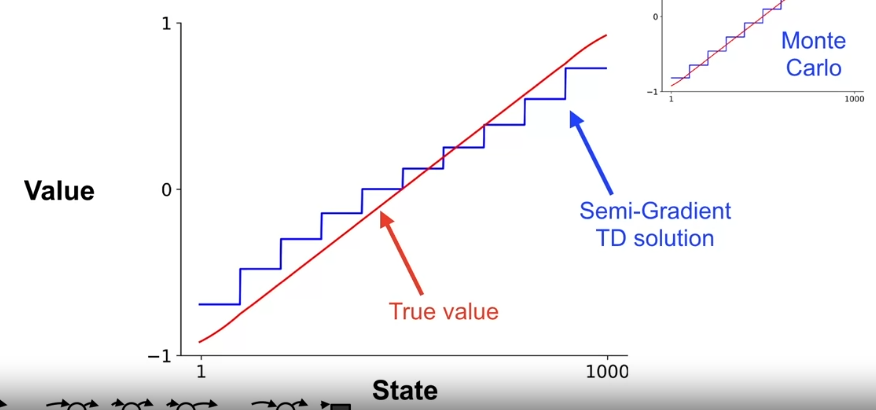
- TD gradient update is biased
- TD runs faster than MC
- Earlier learning is usually more important in practice than long term performance
Linear methods approximation (linear TD)

- Linear in the weights
- x(s) is called a feature vector for state s
- For linear methods, features are basis functions
Update at each time step is

where x_t is just shorthand for x(S_t)
At steady state,
![]()
where ![]()
The weights must converge to satisfy where w_TD is called TD fixed point.
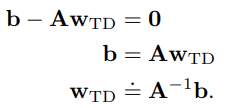
One thought on “Approximate Function Methods in Reinforcement learning”