Tutorial: K-Nearest Neighbor Model

I want to give a quick overview of the K-Nearest Neighbor (KNN) model for beginners into machine learning.

What is KNN?

It’s easy to describe how it works via an example than trying to define it.

We start with tabular data with 2 classes in gender (female and male) and 2 features (height and weight) as follow:

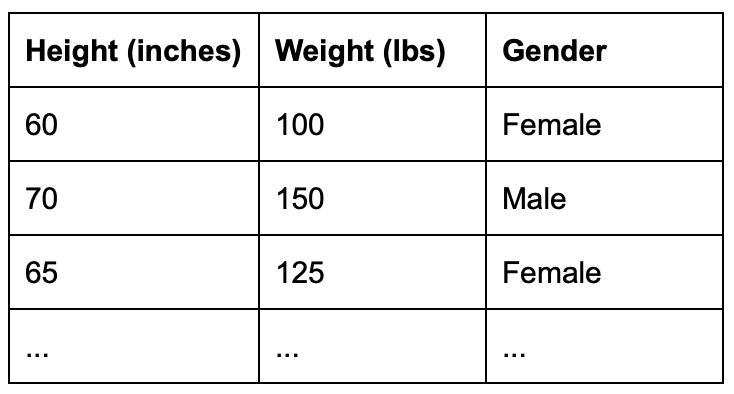
The goals is to build a classification model that take height and weight as input and predict the gender as the output.

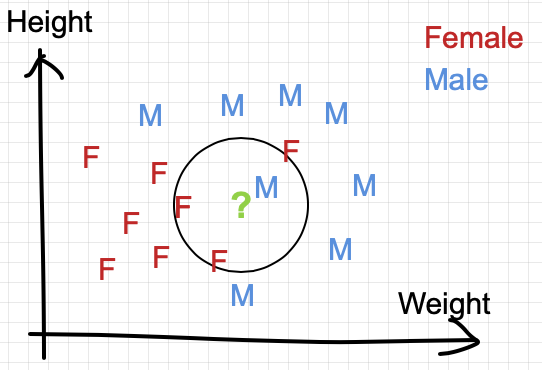
We first plot all these (training) points on a 2-dimensional graph:

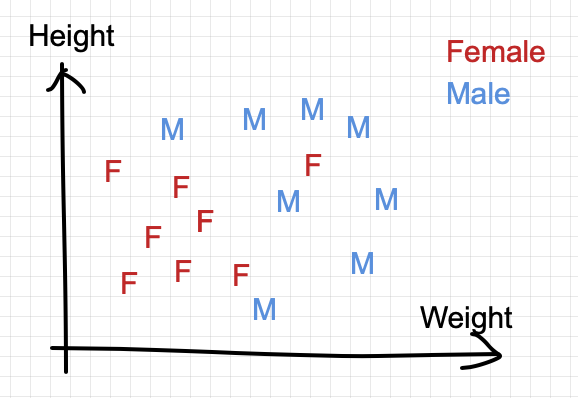
The goal is to predict the class of a testing point in the graph (in green “?” below)

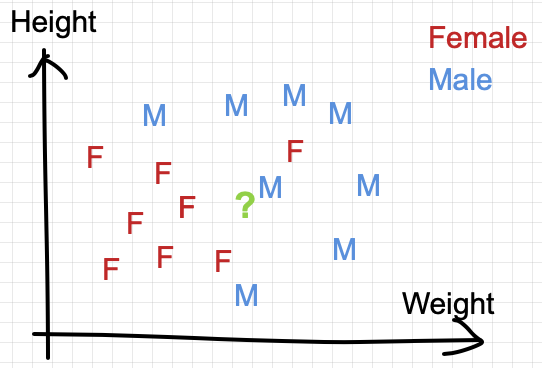
In the simplest setting where k=1, we classify the test point by finding the nearest neighbor in Euclidean distance.

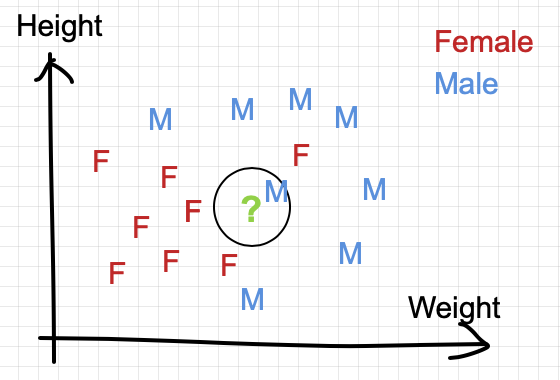
In this case, the test point is classified as Male because the closest neighbor is a training point labeled as Male.

And if we check all the possible points in the entire 2-D space, we can fill up the entire plane to define the decision boundary.

What is the K for?

The k-value in KNN is called a hyper-parameters. In the above example, we set k=1, but if we set k=3, the test point will be classified as below (the 3 nearest neighbor are 2 females and 1 male). This result in a classification of female instead for the test point.

How do you choose the perfect k for your data set? It’s achieve by hyper-parameter tuning with the following heuristic:

• Evaluate the validation or test error rate of the model by varying the k=1,2,3,…
• As k increases, the error rate generally should go down (not always true)
• There should be point where the improving starts to experience diminish marginal return (ie. where a kink/elbow starts on the curve).
• We call the elbow as a choice for k

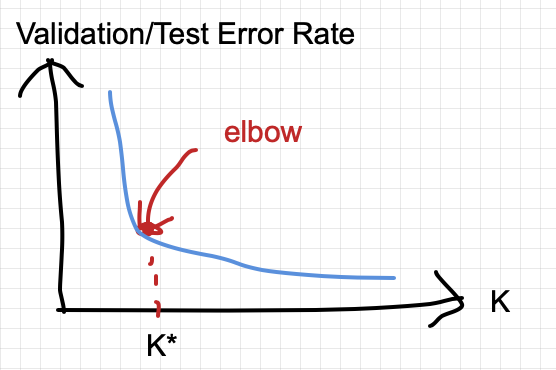
In practice, the curve could be much more noisy and you should pick k based on more experiments.

Why use Euclidean distance?

Using Euclidean distance is common used, but there are many other distance metrics:

• Manhattan distance
• Cosine distance
• Chi-squared distance
• Minkowski distance

You might wonder how to choose the right distance metric. It’s usually chosen experimentally by treating it as hyper-parameter and see which one gives you the best result in the final metric that you can about (ie. Precision and Recall)

One other problem you need to be careful about distance is the difference scales. For example, if you have these 2 features:

• Height (inches)
• Annual Income (dollar)

Annual Income has so much wider range than height that the distance would be dominated by the Annual Income. In practice, you generally want to bring them to similar scales:

• Method 1: standardize each feature dimension (subtract mean and divide by standard deviation)
• Method 2: linearly scale each dimension to be within [0,1] range
• Method 3: cover the features into rank/percentile

What about for multiple classes?

KNN can be generalized to multiple classes (see example for wikipedia)

https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm#/media/File:Map1NN.png

Key takeaways

• KNN is a supervised learning model
  • Each training point has a label.
• KNN is very easy to implement and understand
  • This makes KNN a good base-line model when you first need to tackle a ML problem.
  • You can iterate to more complex model and compare to KNN.
• KNN is a lazy ML model
  • It does not have a training stage. It can direct make prediction based on the data.
  • Contrast to linear regression where the training the model will produce some coefficients and you can forget about the original data.
• KNN does not scale very well on large data set.
  • Since you need to carry your data around for KNN, it slows down when the training data size is large
• KNN suffers from the curse of dimensionality
  • The curse of dimensionality states that at high dimension, any point would have a similar distance to any other point.
  • So all the distance looks alike.
  • This make KNN hard to tell apart which is really the nearest neighbors as there might be many neighbors that are similar in distance.
• KNN is sometimes confused with K-mean clustering
  • Difference 1: K-mean clustering is an unsupervised learning model where you don’t know the labels
  • Difference 2: the k value in KNN is the number of neighbor; the k value in the K-mean is the number of classes