How Transformer Positional Encoding Works

The positional encoding of transformer was a detail added in Attention Is All You Need. When I first saw this, I thought “why is the position oscillating back and forward with these sine and cosine functions”. Below, I try to explain the main ideas because it’s not obvious how it works.

Definition

First the formula of the positional encoding is as followed

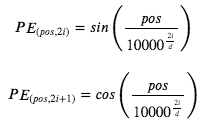
• A Positional Encoding vector has d dimension. The “i” goes from 0 to d/2 so that 2i and 2i+1 fully specified all the indices of the Positional Encoding vector.
• Each word has the raw integer as “pos” in the original sentence
  • Q: why can’t we just use this “pos” as the Positional Encoding?
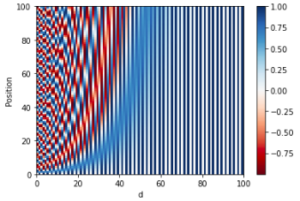
  • Answer: the “pos” can go up to very large value for long sentences, but this absolute index does not help for language learning. For example, does the word “apple” at index 57 different from the same word “apple” at index 92? It does not carry much information, but rather we care more about the relative position between words (will talk about this point more in the rest of this post).
• The 2i and 2i+1 represent the even and odd indices of the Positional Encoding vector of dimension d.
  • Q: Why do we place the sine and cosine function in this alternative fashion in the Positional Encoding vector?
  • Answer: I don’t think it really matters since the individual components(dimensions) of the Positional Encoding vector do not interact with each other.
• Angle – the term inside the sin() and cos() functions
  • It’s the same for every 2 elements of the Positional Encoding vector

Property 1: the L2 norm of the Positional Encoding vector is constant for all “pos”

• This helps to keep the norm to stay the same during dot product

Property 2: the norm of the difference between 2 Positional Encoding vectors separated by k positions is also constant

• This helps to capture the relative distance in the position of words
• This can be considered a shift-invariant property (just like a convolution operation)

Property 3: the Euclidean distance (dot product) of 2 Position Encoding vectors represents the distance (roughly)

• It’s not a strictly monotonic relation where the further the distance of words in the original sentence, the more dot product between 2 Positional Encoding vectors, but it’s mostly good enough.

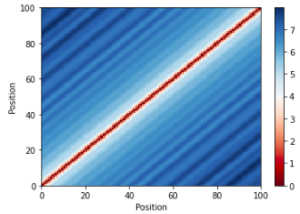
Taking everything to the transformer network

• With all these property in mind, remember the Positional Encoding vector is added to the embedding vector.
  • Q: Why does adding not mess up the embedding vectors?
  • Answer: I don’t have a good explanation other than the fact the the network can optimize and learning in a way that the embedding can share the same vector space with the positional encoding. It’s unclear whether this is the optimal thing to do but we know by experiment this tends to work fine.
• The network will be eventually calculating the component-wise of these vectors indirectly after some transformation by the learning matrices. Conceptually ignore the embedding vector, we can think of the K, Q, V vectors are different transformation of the positional encoding vectors.