Part-of-speech (POS) taggin with Hidden Markov Model(HMM)
What is POS tagging?
Part of Speech (POS) tagging is the process of assigning a part of speech to a word. For example, the sentence “I go home” is tagged as follow
- I (personal pronoun – PRP)
- go (verb – VB)
- home (adverb- RB)
For a list of tags and the abbreviations, see this list from UPenn
Applications
- Name entity recognition – use POS to understand which part of the text needs to be tagged as a named entity
- Coreference resolution – figure out which entity a pronoun refers to in the previous sentense
- Speech recognition – use POS to model the probability of a sequence of words to increase the prediction accuracy
It’s not difficult for human to do if he/she understands the English language, but our goal is to let a machine do it.
What is Markov Chain?
Markov Chain (MC) is an important model used in speech recognition as well as POS tagging. We can fit the POS tag as a state and use it model the state transition probability from one POS tag to another in sentense. In the simple (made-up) example below two just 2 states (tags):

- When the current word is a noun, there is 50% chance that the next word is a verb, and 50% chance that the next word is still a noun.
- When the current word is a verb, there is 90% chance that the next word is a noun, and 10% chance that the next word is still a verb.
In the original example “I go home”, the word “go” is a verb, so the above MC would predict that the word after “go” shoulod have 90% chance being a noun, which would correctly predict the POS tag of “home” because in this case “home” appears after “go”.
In a general graph of MC, there can be any number of states and the transition probabilities are full described between all possible pair of states (a non-possible transition has transition probability of 0).
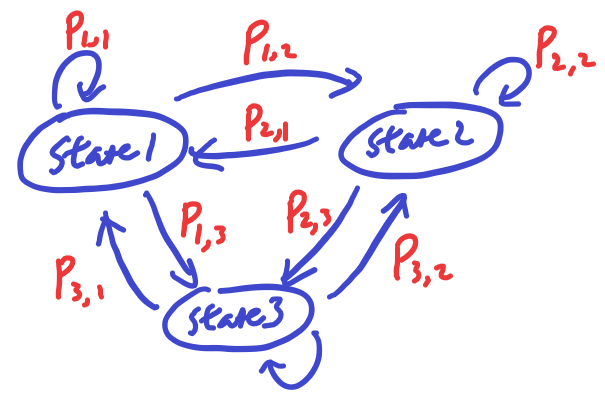
If we have a sequence of POS tags, then we can model a MC to learn about the transition probabilities from the POS tags directly. Unfortunately we don’t directly get the POS tags from most of the text data we can find. We can only observe the words in English, this brings us to use a Hidden Markov Model.
From which state do you start? The initial probability of the first POS tag is given by a vector pi
![]()
What is Hidden Markov Model?
In a POS tagging task, the POS tags is hidden from us (not obervable directly). The Hidden Markov Model (HMM) is more appropriate to model the text data in this case. This hidden part of the model is still the same Markov chain as before, but each hidden state has emission probabilities that define the words that can be emitted/observed from the hidden state.
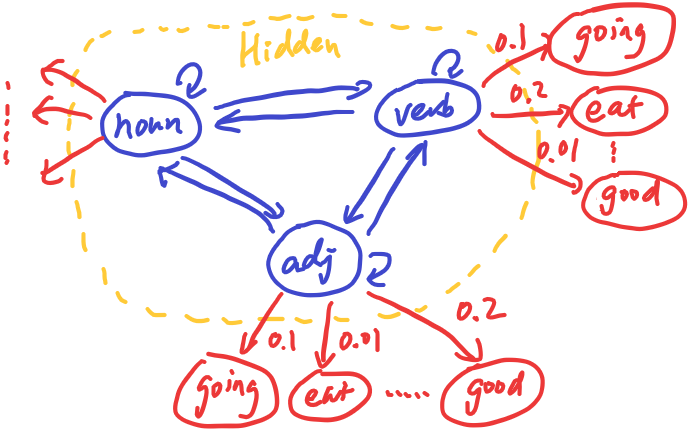
In this diagram, the verb tag has different emission probabilities to the observable words, and these probabilities are different from the adjective tag. (Note the probabilities are made-up in this example)
Recap so far
- Transition probability matrix: describes the probability to going from POS tag to another (all possible pairs)
- Emission probability matrix: describes the probability of observing a word given a POS tag (hidden state)
Given some ground truth about the underlying POS tags of a corpus, it’s quite straight forward to calculate the transition probability and emission probability matrices by counting the number of transition from the corpus. However, when the POS tags are not given to a piece of text, we need some way to infer the POS tags of the text. One way to do this is by the Viterbi algorithm.
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming method, which obtains the “maximum a posteriori probability estimate of the most likely sequence of hidden states” – called the Viterbi path. In other words, it finds the most likely underlying the sequence of POS tags because on the sequence of observed words by choosing the POS tags that maximizes the probability of generating this observed word sequence.
Now let’s lay out the 4 matrices and 1 vector to perform the algorithm:
- Matrix A – the transition probability A(i, j) represents the probability to generate tag_j given tag_i
- Matrix B – the emission matrix B(i, j) represents the probability to generate word_j given tag_i
- Matrix C – the state matrix for Viterbi algorithm to represent the probability of observing the emitted word so far based as of a particular location of the sequence
- Matrix D – the record the most likely tag that produces tag_j at the jth location
- Vector pi – the starting probability of each tag where pi(j) is the probability of tag_j at the start of a sequence
Dimensions
- Matrix A – (number of possible tags, number of possible tags) = (N, N)
- Matrix B – (number of possible words/vocabulary, number of possible tags) = (V, N)
- Matrix C – (number of possible tags, length of the sequence to perform POS tagging) = (N, K)
- Matrix D – (number of possible tags, length of the sequence to perform POS tagging) = (N, K)
- Vector pi – (number of possible tags) = N
Note that Matrix A and B, and Vector pi are given as input to the Viterbi algorithm, so they must be precomputed from a text corpus that has POS annotation. Matrix C and D changes during the algorithm to perform the dynamic programming. Let’s go into how Matrix C and D work below over the 3 steps of the Viterbi algorithm:
- Initialization
- Forward pass
- Backward pass
Viterbi Initialization
The first column of the matrix C is initialized as the probability of emitting word_1 by mutliplying the probability of the starting tag and its associated emission probability with word_1.
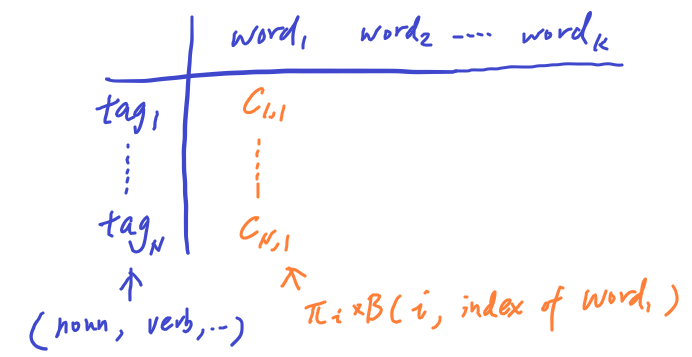
The first column of the matrix D is initialzed to 0 to present the fact that at word_1, there is no tag preceeding the first POS tag.

Viterbi Forward Pass
Next we want to calculate the Matrix C and D from left to right, column by column.
At the 2nd column and 1st row of Matrix C, we calculate the maximium probability of emitting word_2 by doing the below operations:
- Compute joint probability of 3 terms: (1) POS tag probability at the first word, (2) the transition probability from the first tag to the second tag, and (3) emission probability of word2 by the second tag
- We try all N possible tags from the previous tag at word_1, and record the max at c(1, 2)
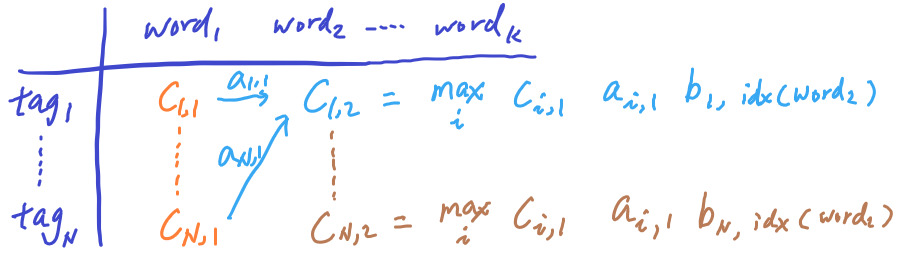
- To fill in the entire column 2 of Matrix C, we need to do this operation over the N possible tags at the 2nd word.
- We can scan the entire matrix from left to right. Matrix C effectively tracks the maximum probability of emitting the current word from each of the POS tag by summarizing probability of observing the previous words before the current word by all the possible POS tags.
At the same time, we also update Matrix D in the forward pass by tracking the specific POS tag that achived the maximum at the corresponding location of the sequence
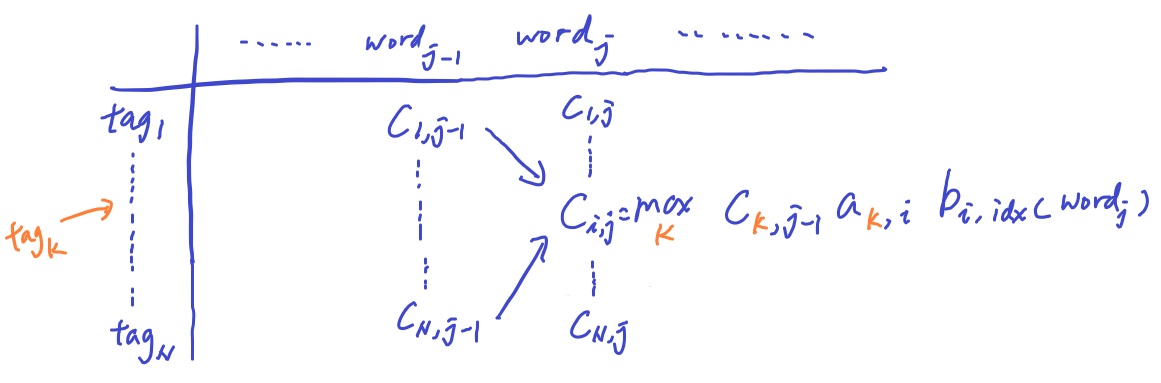
In the maximization process of Matrix C, we are choose over the N tags, so Matrix D is basically the argmax of the same max operation:
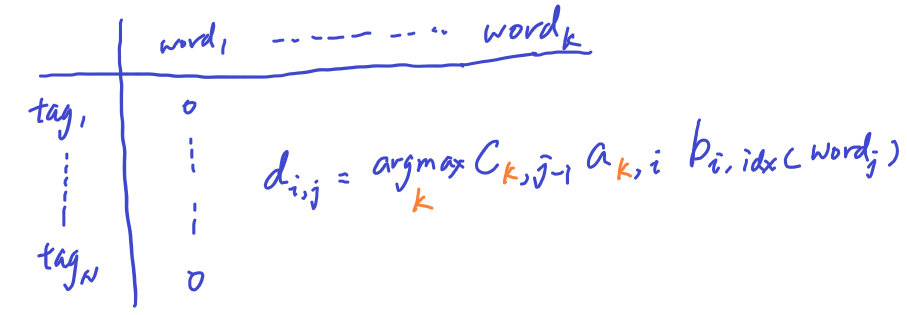
Viterbi Backward Pass
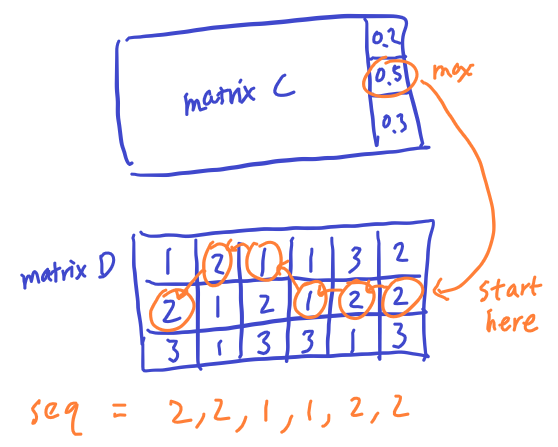
Once the Matrix C and D are fully populated. We can see the sequence that has the highest a posterior probability at taking a look at the largest value in the last column of matrix C.
To find out the entire sequence of POS tags, we just need to backtrace of how we got from the beginning of the sequence to the last column. Luckly we recorded our decision (choice of tag at each maximization step for every column) at Matrix D. The steps can be summarized as below:
- Check the largest value at last column in Matrix C.
- Find the corresponding value at the same location in Matrix D to see which POS tag was used (ex: let’s say tag X is recorded at the correpsonding cell in Matrix D)
- Move left to the previous column in Matrix D and go to the row as suggested the recorded tag.
- Keep moving left on Matrix D to get a sequence of POS tags.
- The result is the reversed sequence of the POS tags used to arrived at the largest probability for the entire sequence.
Conclusion
The Viterbi algorithm is complicated to grasp if you are not familiar with dynamic programming algorithms. Congrats to getting to the end!
You might wonder why we need to go thru all the complication of just figuring out the POS of a word. Can’t we just use a mapping to map a word to a POS tag directly? The problem is some words have multiple meaning and POS tags. For example, the word “go” can be a verb or a noun (as a kind of game). When there multiple of these words in a sentense, it can be complicated to figure out what is best tagging result. POS tagging can be efficiently doing using the Viterbi algorithm because it provided a framework to systematically find that most likely underlying sequence of POS tags that could have generated the observed sequence of words. You probably won’t need to implement it much in practice but understanding it should give you a deeper appreciation of the algorithm.
Improvement
Note that using HMM for POS tagging is not perfect either. There are some assumptions in the model above inherent to the model:
- Word emission probability only depnds on the current POS tag but nothing else.
- POS tag transition probability means each POS tag is predicted by only the previous tag but not the entire sequence.
There are both simplication that make the problem easy to solve, but they are also limitation of the model to understand more complex dependency in the language understanding.