We use text autocomplete everyday, from search engine to writing email. How does the computer know what to suggest as the next word? We will have a quick overview to introduce the concept to understand autocomplete.
N-gram
An n-gram is a sequence of n words. Depending on the value of n, you have unigram, bigram, trigram, etc.
Ex1: I like to play basketball.
- Unigram: “I”, “like”, “to”, “play”, “basketball”
- Bigram: “I like”, “like to”, “to play”, “play basketball”
- Trigram: “I like to”, “like to play”, “to play basketball”
- N-gram: …
N-gram probability
Suppose we keep track of the count of all the unigrams and bigram from a text corpus.
We can ask question like what is the probability that the work “basketball” appears after “play”
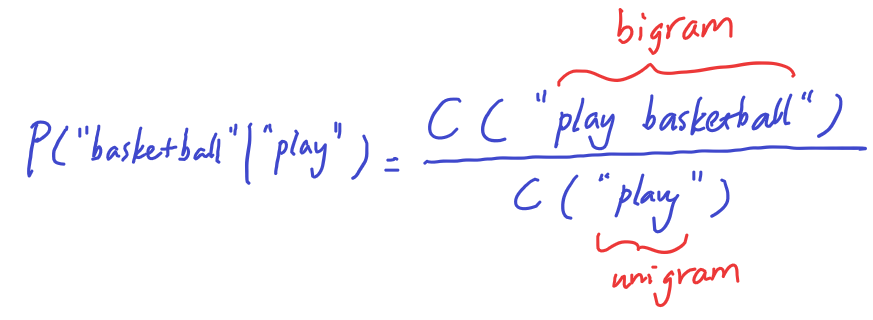
Sequence probability
To find the probability of an entire sentence, we can apply the conditional of each word based on the entire sequence seen before it using Bayes Rule.
- P(B|A) = P(A, B) | P(A)
- P(A, B) = P(A)*P(B|A)
For a long sequences
- P(A, B, C) = P(A) * P(B,C|A) = P(A) * P(B|A) * P(C|A,B)
- P(A, B, C, D) = P(A) * P(B|A) * P(C|A,B) * P(D|A,B,C)
To apply it to the sentense “I like to play basketball”
P(“I like to play basketball”) = P(“I”) * P(“like”|”I”) * P(“to” | “I like”) * P(“play” | “I like to”) * P(“basketball” | “I like to play”)
where all the conditional probability can be express by the ratio of count as shown in earlier section (ex: P(“like”|”I”) = C(“I like”) | C(“I”)
This direct probability model above has some problems:
- The term P(“basketball” | “I like to play”) requires calculating the count of “I like to play” which is 4-gram and P(“I like to play basketball”), which is a 5-gram
- It’s very hard to collect enough data about 4-gram and 5-gram.
- When you train a model using a training corpus, it will like be difficult to cover all the possible 4-grams and 5-grams that will be encountered in a new piece of text not from the training corpus.
- In that case, the count of the 4-gram and 5-gram will be 0, resulting in 0 divided by 0 when trying to calculate the conditional probability
- On the other hand, unigram and bigram have much higher coverage because there aren’t an many uniqe bigrams and 4-grams.
As a simplication, we can use bigram to model the same sentense as an approximation:

This result in
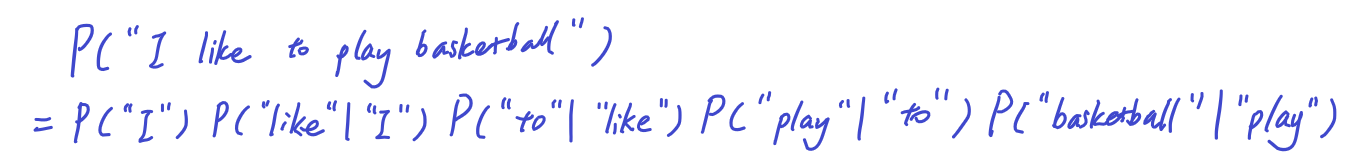
Start and end tokens
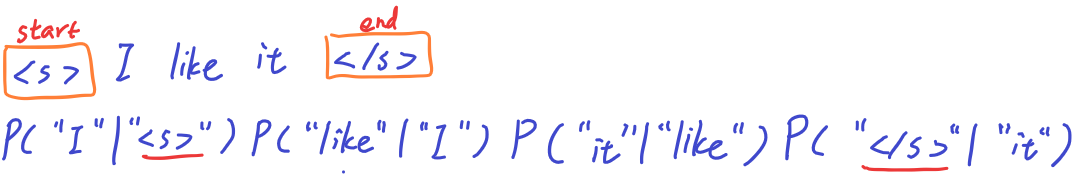
- The start token fixes a problem of having to model the first word differently with a marginal probability. Instead, a conditional probably can still be used
- The end token helps to model the probability of sentenses of different length because other it’s not possible to compare the probability of sentenses of different length.
- This can be extended from bigram to trigram by appending extra start token in the front and end tokens at the end.
N-gram language model
A language model can be built by calculate the all these conditional probability from a corpus of text. This is essentially a probability matrx: P(next_word | current_word) where next_word and current_word are all the possible words in the vocabulary. This language model can:
- Predict the next word given current word
- Calculate the probability of a sentense
- Generate text by sampling the next word from the probability matrix. Start with the start token <s> and keep going until the end token </s> is encountered.
Perplexity – evaluation of language model
The word perplexed refers to the case when someone is confused by something that is complex. So perplexity is kind of like the complexity of a piece of text. Specifically, a piece of text written by human is less perplex than a piece of randomly generated text.
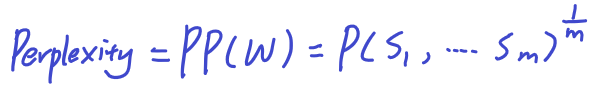
- W is the entire set of m sentences
- m is the number of sentences in the set
- each s_i is the i-th sentence in W
Applying this to a bigram model:
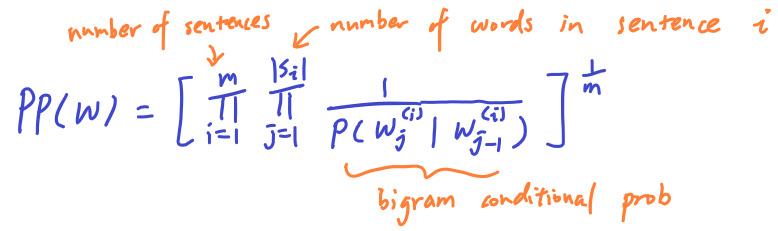
- Observation: since the probability is in the denominator, higher probability gives lower perplexity.
Handling Unknowns with Smoothing
Out of vocabulary
- In testing time, you will inevitably encounter words that you have not seen before, by then you can either drop that word or use <UNK> to represent this unknown word.
- By definition, an unseen words would have 0 probability, this also causes the probability of th sentence to become 0 (see formula in the sequence probability)
- For words that are rare in the training corpus, we might choose just use the token <UNK> to save memory if there are too many words in the corpus
Missing N-gram
- An n-gram in the test data might not be encountered during training will be predicted with 0 probability (see formula in the sequence probability)
- This causes the probability of the entire sentence to become 0.
The solution to the above problems is smoothing, which is a technique to avoid getting a 0 probability.
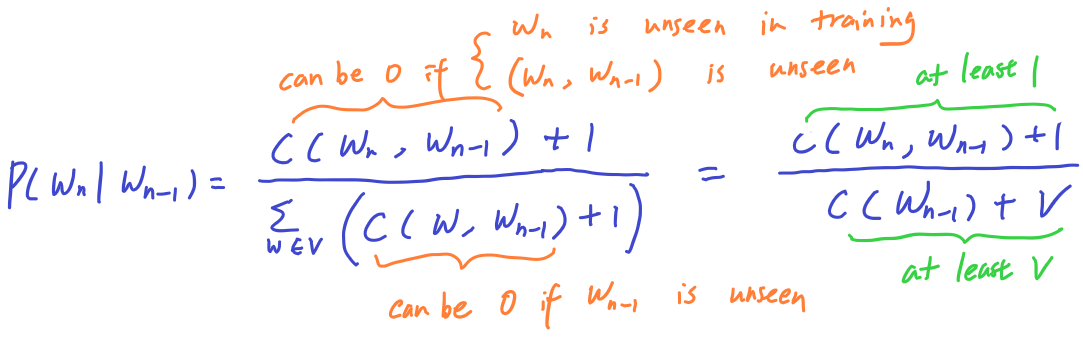
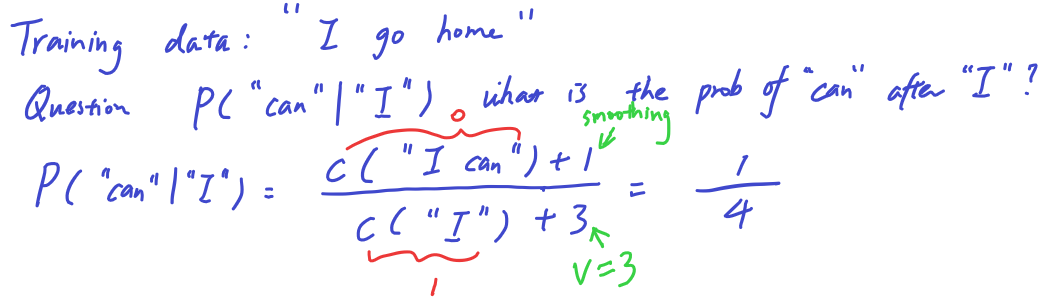
For example,
Another strategy is using backoff:
- If N-gram is missing from the trained model, then try (N-1)-gram. If (N-1)-gram is also missing, then try (N-2)-gram.
- When backing off, we don’t want to directly use the lower gram probability direclty, but we should apply a discounting to the probability (ex. Katz backoff)
- Use a discount factor of 0.4 is a good starting choice to experiment
One more strategy is to interpolate the probability of all the lower order N-grams when a particular N-gram is missing.
Putting everyting together
So the N-gram model is a language model that can be used to build a autocomplete system. By choosing the next word that maximizes the probability of a (N+1)-gram sequence given the current N-gram sequence.
In this article we showed how to apply the n-gram model at the word level, but it’s also possible to apply this model at the character level. Of course this is not the only way to build an autocomplete system, but it’s the fundamental concept used in most autocomplete system today in search engine, and recommendation system.